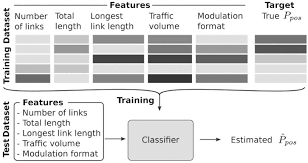
The training data are labeled:

We have a set of instances represented by certain features and with a particular target attribute

The features are also called predictors or independent variables (X)

The target is also known as dependent variable or outcome (Y)

I.e. we have historical data with mapped input => output pairs

the goal

approximating a mapping function (g) from input variables (X) to output variable/s (y).

$$ {g:X\to Y} $$

The job of modeling algorithm is to find the best mapping function, such that will minimize the error on prediction.

Problems that solves

Two main problems categories:

classification

predicting a discrete class label output for an example.

example: determining if an email is spam or not

regression

predicting a continuous quantity (value) output for an example.

example: predict the price of a house

classification tasks

The Process

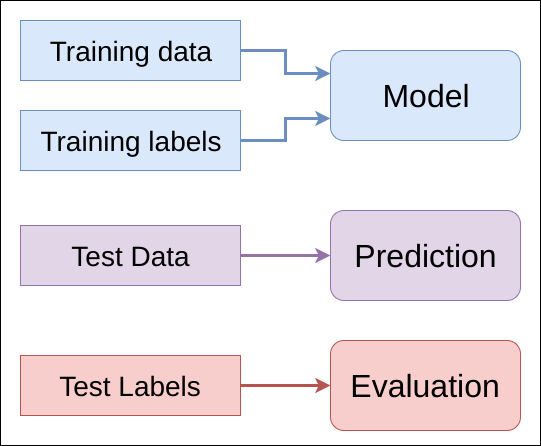
You can use this ML_Process_Template.ipynb for a starting point.

Given is a set of ${N}$ training data of the form:

$$ {(x_{1},y_{1}),...,(x_{N},\;y_{N})} $$

Where ${x_{i}}$ is the input (feature) vector

All Supervised Learning algorithms seeks a function:

$$ {g:X\to Y} $$

Where

${X}$ is the input (feature) space

${Y}$ is the output (target) space

${g} \in {G}$, ${G}$ represents the hypothesis space (see What exactly is a hypothesis space in the context of Machine Learning?)

Scoring function

In ML, ${g}$ is represented using a scoring function

${f:X\times Y\to {\mathbb {R} }}$

such that ${g}$ is defined as returning the ${y}$ value that gives the highest score

$${\displaystyle g(x)={\underset {y}{\arg \max }}\;f(x,y)}$$

Loss function

In order to measure how well a function fits the training data, the loss function is defined:

$$L: Y \times Y \to \Bbb{R} ^{\ge 0}$$

I.e. if we have the training samples ${(x_{i},\;y_{i})}$, then the the loss of predicting the value ${{\hat {y}}}$ is ${L(y_i,\hat{y})}$.

Usually, in the same context, is used the term cost function, which can be regarded as a generalization of the lost function

Feature Selection

Features are chosen with a specific task in mind

Curse of Dimensionality: The more features you include, the more data you need (exponentially) to produce an equally accurate model

No Free Lunch' theorem

'No Free Lunch' theorem: "If an algorithm performs better than random search on some class of problems then it must perform worse than random search on the remaining problems".

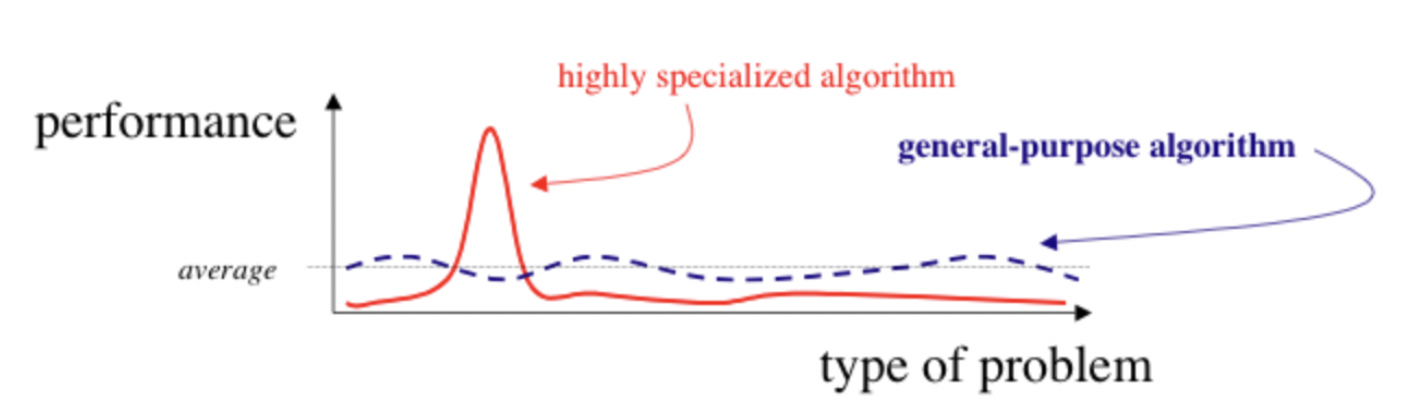
Generalization

The ability of algorithm to perform well on new (not-seeing before) data

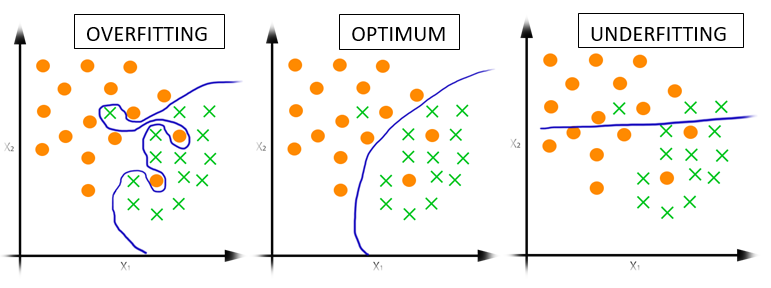
Overfitting and Underfitting

Overfitting happens when a model learns all the detail (and noise) in the training data to the extent that it negatively impacts the performance of the model on new data.

Underfitting is the case where the model has "not learned enough", resulting in low generalization and unreliable predictions.

Overfitting and underfitting are the two biggest causes for poor performance of machine learning algorithms

Overfitting vs Underfitting

Bias and Variance

Bias is the difference between the estimator's expected value and the true value of the parameter being estimated. In ML, biased results are usually due to faulty assumptions

In ML, bias is inevitable - remember the 'No Free Lunch theorem'.

Variance is the expectation of the squared deviation of a random variable from its mean.

The Bias–Variance tradeoff

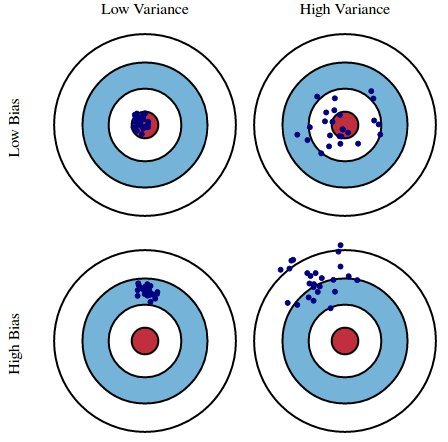
The Bias-Variance Tradeoff by Giorgos Papachristoudis

Cross-validation

Cross validation is a technique for testing the effectiveness of a machine learning models.

Cross validation can give an insight on how the model will generalize to an independent dataset

The goal of cross-validation is to test the model's ability to predict new data, that was not used in estimating it, in order to flag problems like overfitting